
Those of us in the high-performance industries are always in the pursuit of better performance from the machines we build. We spend countless hours engineering, analyzing, testing, and squeezing every bit of performance that we can from the parts and materials available. We chase perfection from every means necessary because a win or loss can be the difference of a tenth of a second.
When a tenth of a second matters, every ounce of weight makes an entire world of difference.
Over the years, material science has advanced, and so has our ability and desire to reduce weight. Materials like Advanced High Strength Steels allow us to build lighter yet stronger chassis then those of past generations. While some builders maximize these benefits by building lighter and stronger chassis, many must meet minimum weight requirements for their cars to participate in certain racing series. While some builders may look at these weight requirements as a hindrance, the best ones use it to their advantage. These builders design their chassis with cross-sectional weight in mind, selecting materials and sizes to optimal strength-to-weight ratios.
Theoretical Weight vs. Actual Weight
It is essential to be aware in the design process that the Theoretical Weight may be slightly different from the Actual Weight of material. This is because theoretical weight is calculated by measuring nominal dimensions (volume) and density, and does not account for the allowable manufacturing deviations. All metal materials are produced within a standard tolerance and deviations are allowable, meaning the actual weight can be more or less than the theoretical weight. Actual weight can only be obtained by weighing the material with a scale.
Material Densities
| Material | lbs. / cubic in. | lbs. / cubic ft. | gm. / cubic cm. |
|---|---|---|---|
| Steel & Stainless Steel | 0.284 | 3.4032 | 7.870 |
| Aluminum | 0.098 | 1.1760 | 2.710 |
| Titanium | 0.163 | 1.9560 | 4.506 |
| Lead | 0.410 | 4.9200 | 11.360 |
Density may vary slightly by each grade of material depending on the alloying elements.
In general, the density of steel is in the range of 0.284 to 0.291 lbs. / in3 while stainless steels (such as 304) and tool steels (such as T1 and M2) have densities at the high end of that range and mild steels, alloys (such as 4130) and Advanced High Strength Steels (such as Docol® and Strenx®) have densities at the low end of that range.
Aluminum densities also do not vary much at all with a range of 0.096 to 0.101 lbs. / in3. High strength grades such as 7075 and 2024 have similar densities at or over 0.100. Common grades like 6061, 5052 and 3003 all have densities under 0.098.
Theoretical Weight Formulas
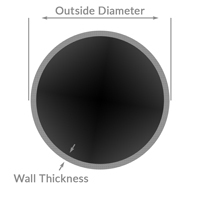
Round Tube
lbs. / ft = (Density x π) x (O.D. – wall thickness) x wall thickness
Example: lbs. / ft for 1.25 O.D. x .065 wall 4130
(3.4032 x π) x (1.25 -.065) x .065 = 0.8226 lbs. / ft

Square & Rectangular Tubes
lbs. / ft = (Density x 4) x [(width + height) / 2 – wall thickness] x wall thickness
Example: lbs. / ft for 1 x 2 x .065 MS EW
(3.4032 x 4) x [(1 x 2) / 2 - .065] x .065 = 1.269 lbs. / ft
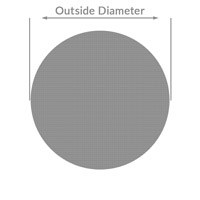
Round Bars
lbs. / ft = (Density x .786) x diameter
Example: lbs. / ft for 1.50 6061-T6
(1.176 x .786) x 1.502 = 2.078 lbs. / ft
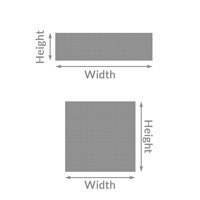
Flat & Square Bars
lbs. / ft = Density x width x height
Example: lbs. / ft for 1 x 2 6061-T6
1.176 x 1 x 2 = 2.352 lbs. /ft
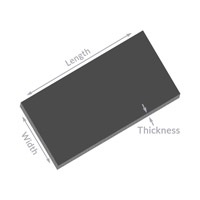
Sheets
lbs. / sq. ft = Density x thickness x 12
Example: lbs. / sq. ft for .063 6061-T4
1.176 x .063 x 12 = 1.270 lbs. / sq. ft
Hex Bars
lbs. / ft = (Density x .866) x diameter2
Example: lbs. / ft for .625 304 Stainless Steel Hex Bar
1.176 x .063 x 12 = 1.270 lbs. / sq. ft


